L’essor récent de l’intelligence artificielle générative (IA Gen) redéfinit la manière dont les assureurs construisent et interprètent leurs modèles de risque. Plébiscitée pour sa capacité à produire automatiquement des scénarios quantitatifs, des réponses aux questions complexes ou des images, l’IA Gen peut également mieux extraire et structurer des informations issues de documents (rapports financiers, dossiers sinistres, articles scientifiques, etc.) en comparaison à ce qu’il était possible de faire il y a quelques années en traitement automatique du langage.
Quelles limitations en assurance et actuariat ?
Malgré ces avancées, la manière d’appréhender la connaissance dans le secteur de l’assurance présente encore des limites notables. Les pratiques usuelles, notamment en actuariat, reposent encore largement sur :
- Des sources limitées : les informations brutes exploitées pour les calculs actuariels sont généralement des sources internes, partielles et dont la qualité n’est pas toujours contrôlée.
- Des formats tabulaires figés : la quasi-totalité des indicateurs (sinistres, expositions, montants provisionnés…) sont organisés dans des bases relationnelles, perçues comme immuables, quantitatives et difficiles à enrichir avec de l’information contextuelle.
- Une agrégation arbitraire : pour réduire la dimensionnalité, on agrège fréquemment les observations de manière homogène par région ou population, sans exploitation fine des regroupements entre variables et observations.
- Des corrélations simplistes : on cherche surtout des liens linéaires ou temporels, au détriment d’interactions complexes (causes, effets de seuil, rétro-actions, effets latents).
Ces limites ont un impact direct sur l’estimation du risque, par exemple lors de calculs actuariels en tarification ou en provisionnement, qui dépend largement de la richesse et de la structure des connaissances sous-jacentes. Elles freinent également les solutions qui peuvent être proposées pour atténuer les risques : compréhension des mécaniques de préventions relatives à certains facteurs, ventes croisées permettant une meilleure couverture de l’assuré, etc. Par exemple, en assurance responsabilité civile médicale, l’exploitation automatique d’un dossier de rapports médicaux et d’expertises permettrait de reconstituer la chaîne causale des soins et d’évaluer précisément la responsabilité des praticiens – une tâche aujourd’hui réservée à de longues phases d’investigation humaine. De même, en assurance énergie, la limitation à une dizaine de variables descriptives pour caractériser un sinistre pénalise la génération d’hypothèses robustes sur la durée et le montant des provisions, ainsi que la définition de mesures d’atténuation proactives.
Quels procédés pour structurer et exploiter ces données ?
Dans la suite de cet article, nous présentons une approche basée sur la génération de graphes orientés acycliques (DAG) par IA générative, afin de mieux structurer la connaissance causale et répondre aux enjeux actuels de compréhension du risque. Cette approche se décompose en deux phases : d’une part, la structuration et la consolidation exhaustive des informations ; d’autre part, l’exploitation de ces DAG pour enrichir les calculs actuariels et les scénarios de risque.
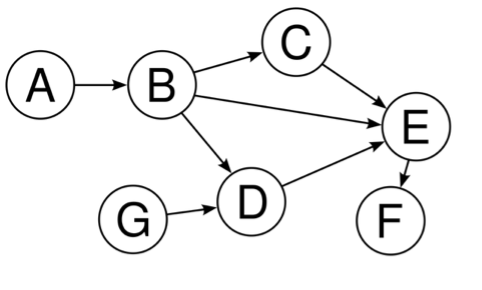
[1] Exemple imagé de DAG.
La première partie des travaux consiste à transformer l’ensemble des données non structurées – rapports d’expertise, dossiers médicaux, plans techniques, etc. – en un référentiel exploitable de manière cohérente et traçable. L’idée est d’abord de formaliser chaque événement repéré dans les documents sources comme un nœud de graphe, et chaque lien de causalité comme une arête. Pour garantir une extraction cohérente, ce formalisme est directement codé via un schéma de données précis, imposant une validation automatique des données produites. Au démarrage du processus d’acquisition [2], les documents sont classés, enrichis de balises d’annotation uniques puis découpés en segments de taille fixe – les « chunks » – afin de maîtriser tant la granularité que la traçabilité des informations transmises aux grands modèles de langage (LLM).
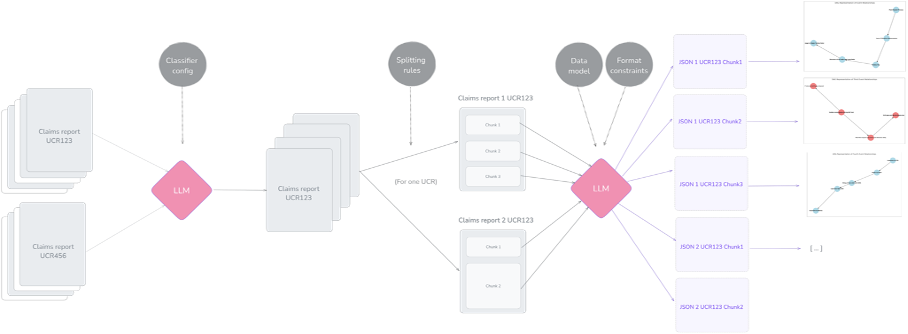
[2] Premières étapes du processus d’acquisition.
Chacun de ces chunks génère, via un LLM, un chunk graph conforme au schéma. Conscients des limites des LLMs lorsqu’il s’agit de fusionner simultanément un grand nombre de graphes (phénomène dit de « lazy LLM »), nous avons mis en place une fusion progressive : les graphes intermédiaires sont agrégés par petits lots, jusqu’à constituer un graphe unifié. À chaque opération, les métadonnées d’origine restent attachées à leur nœud, assurant une transparence totale. Un module de post-traitement algorithmique vient ensuite compléter la fusion, réintégrant finement les métadonnées et corrigeant les pertes d’information. Le graphe final, fusionné, est ensuite standardisé automatiquement : un algorithme de regroupement met ensemble les valeurs de propriétés équivalentes (par exemple, « Bush Fire » et « Fire » sont unifiés en « Fire »), et unestandard map conserve l’historique de ces transformations. Cela termine le processus d’acquisition [3].
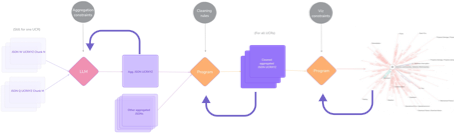
[3] Dernières étapes du processus d’acquisition.
On intègre le graphe ainsi uniformisé dans une base orientée graphe, où chaque nœud événement (Event) est doublé d’un nœud Metadata centralisant ses attributs, tandis que des nœuds dédiés retracent l’appartenance aux claims et aux documents sources. Ce dispositif permet la génération dynamique de métagraphes [4], agrégats d’événements selon des critères macro, pour des analyses à plus grande échelle.
Pour valider l’efficacité de ce processus, nous avons défini un jeu de métriques : le nombre total de nœuds créés, le taux de compression moyen (capacité à regrouper les nœuds redondants), le pourcentage de déduplication, le ratio de pertes lors des fusions successives et le taux de propriétés manquantes. Chacune de ces mesures est calculée automatiquement, offrant un retour à la fois quantitatif et qualitatif, indispensable pour piloter l’optimisation continue de notre pipeline d’extraction et s’assurer de la cohérence du Claim Graph final. D’autres méthodes d’évaluations dites « human in the loop » ont également été implémentées.
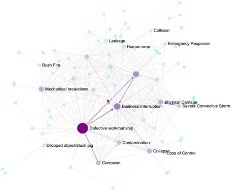
[4] Exemple de métagraphe.
La seconde partie des travaux repose sur l’exploitation des graphes, notamment pour des calculs actuariels. Une fois le référentiel déterminé, l’enjeu est de rendre ces connaissances interrogeables et interprétables. Des moteurs de traduction de requêtes en langage naturel vers un langage de graphe formel (Cypher) ont d’abord été développés : ils convertissent automatiquement une question métier (« Quel est le coût moyen induit par la panne d’une turbine d’un site pétrochimique au Brésil ? ») en requête structurée. Cela sert aussi bien à filtrer un graphe qu’à réaliser des calculs (nombre de nœuds, calculs sur attributs, etc.) à la façon d’une requête SQL et à se servir des informations de ce graphe dans le cadre d’une approche de génération augmentée par récupération (RAG) souvent utilisée pour les agents conversationnels [5]. L’évaluation systématique du temps de réponse, de la recevabilité qualitative des résultats et des indicateurs de précision/rappel assure la robustesse de l’approche.
Des outils graphiques ont été expérimentés : nuages de points pour observer des groupes de dénomination pour

[5] Requête en langage naturel à un agent conversationnel via Cypher.
mieux les standardiser, diagramme en coordonnées parallèles pour la distribution des événements chronologiques [6]. Un système de recommandations pour rapprocher des chroniques d’événements similaires ou des contextes similaires a également été développé en se basant sur une approche de regroupement sémantique par plongement vectoriel.
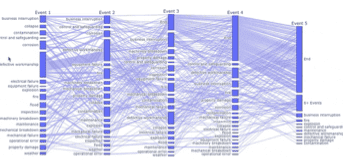
[6] Représentation de codistributions d’événements organisés chronologiquement.
L’intégration du métagraphe de connaissance causal, dans les calculs actuariels traditionnels, ouvre également de nouvelles perspectives pour des méthodes de tarification non-vie (calculs prime pure), pour l’estimation de certains paramètres de provisionnement (segment, années de développement, coefficients de passage notamment), d’autres simulations « as if » basées sur l’impact de scénarios hypothétiques propagés à travers le graphe causal.
Supposons un graphe causal, composé de nœuds (événements) reliés par des arêtes (relations causales). Chaque événement possède une fréquence d’occurrence et un coût moyen associé. Par exemple, une panne (événement C) peut entraîner un accident (événement A), lui-même à l’origine d’une réparation (événement B) [7]. Le graphe causal est traduit en une matrice de transition probabiliste, dont chaque élément représente la probabilité qu’un événement en déclenche un autre. En partant d’un vecteur initial d’occurrence des événements, on calcule récursivement le nombre moyen d’occurrences attendu par contrat. En sommant ces résultats et en multipliant par les coûts moyens, on obtient une première prime pure estimée (très simpliste). Il est aussi possible de prendre en compte les spécificités contractuelles (exclusions, garanties, critères) via une adaptation du graphe : exclusion d’événements en supprimant leur probabilité initiale ou leur coût moyen, filtrage démographique entraînant le recalcul des probabilités de transition.
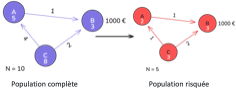
[7] Exemple de formalisme pour l’usage de métagraphes pour le calcul d’une prime pure.
Plusieurs vérifications sont néanmoins nécessaires pour mener à bien de tels calculs : Propriété de Markov faible (indépendance des transitions successives), indépendance des événements issus du même nœud source, unicité des sources pour chaque événement, coût individuel par nœud estimé correctement viasystème d’équations linéaires, etc.
Quelques chiffres avec un exemple ?
Pour matérialiser notre démarche, plusieurs expérimentations ont été menées auprès de différents assureurs en France et à l’étranger. Nous revenons ici sur l’une d’entre elles en ayant pris soin de masquer les données confidentielles. L’information source correspond dans ce cas à des dossiers sinistres en assurance de spécialité sur le risque énergie.
Ces dossiers sources sont particulièrement intéressants, car ils intègrent le contexte client, la chronologie des faits, l’impact financier, les avis d’experts et les interventions juridiques. Par ailleurs, chaque sinistre évolue selon plusieurs phases : déclaration initiale, puis rapports successifs (parfois jusqu’à trois), reflétant l’accumulation progressive de connaissances et des conséquences financières associées.
Le schéma de données, coconstruit avec des experts et un LLM, regroupe près de 90 attributs par sinistre, arête ou événement. Pour traiter cet éventail d’informations, nous avons retenu une combinaison de plusieurs modèles, notamment : un Llama 3 8B pour les tâches simples, telles que la classification des segments textuels, un Clause Sonnet 3.5 pour l’inférence causale et un Phixtral multimodal pour l’intégration des tables et images dans la représentation sémantique. Grâce à l’architecture agentique décrite précédemment, la création d’un graphe complet se fait en moyenne en 1,5 minute par dossier, pour un coût de quelques euros seulement.
Appliquée à plus de 2 000 dossiers sinistres, cette technique nécessite des optimisations (parallélisation des traitements, stratégies asynchrones et orchestration), mais permet de générer en continu un référentiel de graphes causaux qu’il est ensuite possible de stocker dans des bases de données telles que des Neo4j.
Enfin, les premières applications pratiques ont révélé une bonne efficacité opérationnelle du processus : le regroupement des graphes nécessite rarement plus de deux à trois itérations. En moyenne, chaque sinistre est représenté par un graphe composé de 5 à 12 nœuds événements. La méthode montre également une excellente capacité de déduplication, dépassant souvent 60 % lorsqu’il existe une redondance entre les graphes intermédiaires. Par ailleurs, le niveau de complétude des attributs est remarquable, supérieur à 90 % dans les données traitées. Sur le plan actuariel, les résultats sont en cours de validation comparative avec les techniques usuelles. La précision des hypothèses, notamment sur les années de développement et les segments de risque, s’avère déjà très prometteuse.
Quelles conclusions et perspectives ?
Ce cas d’étude permet de mettre en exergue les apports de l’IA Gen pour la connaissance assurantielle et actuarielle. L’exploitation contrôlée et structurée des LLM via un protocole itératif, contrastant avec les usages directs et non contraints courants, permet d’obtenir des informations robustes rapidement. Il garantit une traçabilité totale grâce à l’association systématique de chaque nœud Event à son nœud Metadata, offrant transparence et auditabilité à chaque étape du traitement. Par ailleurs, la logique de standardisation automatisée reposant sur une méthodologie hybride, appliquée aux attributs événementiels, assure une homogénéité reproductible et déployable à grande échelle. Enfin, l’interaction agentique (text-to-Cypher) permet aux actuaires et aux décideurs métiers d’interroger directement le graphe en langage naturel, sans connaissance technique préalable.
Comparée aux approches existantes – souvent ponctuelles, symboliques ou black-box et limitées en volumétrie –, cette solution hybride (LLM contraints + itérations structurées + calculs sourcés) ouvre la voie à une interprétation des risques à la fois fiable, reproductible et scalable, offrant un socle robuste pour la gestion d’informations multisources en actuariat.
La démarche présente toutefois certaines limites. D’abord, la sélection des informations reste perfectible : la mise en place de filtres sémantiques avancés ou de mécanismes d’apprentissage supervisé pourrait affiner la pertinence des extraits retenus. Par ailleurs, les structures de modèles de données déployées gagneraient à être davantage abstractisées, pour assurer une portabilité fluide du schéma entre contextes métier variés (l’organisation d’une connaissance du parcours de soins patient n’a pas la même forme que le déroulé d’un sinistre transport). De plus, le format de données de sortie, bien que riche et structuré, impose une conduite du changement au sein des équipes métiers et actuarielles, nécessitant des formations dédiées, la création de nouvelles responsabilités et des ajustements organisationnels. Enfin, les méthodes d’évaluation actuelles demandent à être renforcées : l’élaboration de protocoles opérationnels standardisés et d’indicateurs quantitatifs plus fins est cruciale pour mesurer rigoureusement la fiabilité et l’impact opérationnel de la solution. Ces perspectives constituent autant d’axes de travail futurs pour rendre l’approche non seulement plus efficiente, mais également plus immédiatement intégrable dans un environnement actuariel en constante évolution.
